Graphical Abstract

Abstract

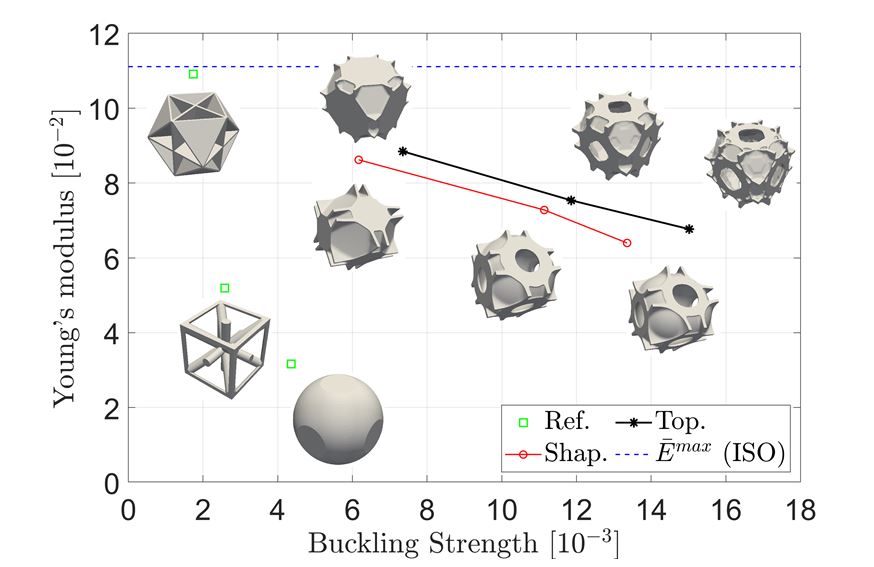
Materials with extreme mechanical properties are desirable for many applications. Stiffness and strength are fundamental properties for determining material load-bearing capability. Stiffness accounts for the ability to resist deformation, while strength measures the ultimate load-carrying capacity. Material geometry strongly dictates material properties. Many studies have focused on exploring materials with optimal stiffness by carefully tailoring material geometries via free topology optimization methods. However, recent research has shown that isotropic stiffness-optimal plate material is inferior from a bucking strength point of view compared to the isotropic truss counterparts for the same volume fraction [1]. Assuming small strains and ignoring material and geometric nonlinearities, topology optimization methods have been employed to systematically design 2D materials with enhanced buckling strength for different macro-level stress situations [2]. Based on the small deformation theory, material stiffness is evaluated using the homogenization method. Buckling strength under a given macroscopic stress state is estimated using linear buckling analysis with Block-Floquet boundary conditions to capture both short and long wavelength buckling modes. This study extends 2D material design with enhanced buckling strength in [2] to 3D material design with tunable stiffness and buckling response [3]. The optimization problem is formulated to maximize the weighted stiffness and buckling response. A class of 3D isotropic materials is designed to achieve tunable stiffness and buckling response by assigning different weight factors for stiffness and buckling strength under uniaxial compression. Moreover, inspired by the topology optimized material configurations, a subsequent feature-based shape optimization approach is employed to simplify material geometries. In the feature-based approach, material architectures are parametrized using several hollow and one solid super-ellipsoids.  Compared to stiffness-optimal closed-cell plate material, the material class reduces Young's modulus to a range from 79% to 58% and improves the uniaxial buckling strength to a range from 180% to 767%. Both topology and shape optimized results demonstrate that material buckling strength can be significantly enhanced by allowing curved plates and member thickening

Keywords

Buckling strength, stiffness, topology optimization, shape parameterization.

Acknowledgement

We acknowledge the financial support from the Villum Fonden through the Villum Investigator Project InnoTop.

References

1. Andersen, M.N., Wang, F. and Sigmund, O., Materials & Design, 2020, 198, p.109356.
2. Thomsen, C.R., Wang, F. and Sigmund, O., Computer Methods in Applied Mechanics and Engineering, 2018, 339, p. 115-136.
3. Wang, F. and Sigmund, O., 2020, arXiv preprint arXiv:2012.01359.

Biography

Fengwen Wang is a senior researcher at the Department of Mechanical Engineering, Technical University of Denmark (DTU). She obtained her Ph.D.-degree in 2012 and her Ph.D. Thesis won Ph.D thesis of the year in DTU, 2013. She is an expert in large scale numerical simulations and topology optimization, including structural and material designs, and optical device designs. Her scientific focus areas include:

• Computational mechanics, large scale numerical simulations and structural optimization
• Flexible material and structure designs considering geometrical and material nonlinearity
• Optimization of material and structure with enhanced stiffness and strength responses
• Numerical simulation and optimization for nonlinear dynamics
• Numerical simulation of multi-physical problems
• Applications of topology optimization in multi-physical problems and in various research fields
• Optimization of optical devices, e.g., slow light waveguides, small cavities, topological insulator etc.